Lud­wig Bieber­bach ließ seine Zigarette sinken, als es klopfte. Er stieß die über­flüs­sige Asche mit einem Ruck ab und ver­ankerte die ger­ade erst anger­auchte Kippe in ein­er der drei Ein­fas­sun­gen des Porzel­lan-Aschen­bech­ers mit dem konzen­trischen Logo der Uni­ver­sität zu Berlin darauf, wo sie knis­ternd weit­er bran­nte. Er stand von seinem Schreibtisch auf, brachte seine Noti­zen in Ord­nung, richtete sein Jack­ett, entsch­ied sich nach kurzem Über­legen dage­gen zu lüften (der Dekan ver­suchte neuerd­ings eher erfol­g­los die Anti-Rauch­er-Geset­ze der Partei durchzuset­zen) und öffnete Theodor Vahlen die Tür zu seinem Büro. Sie begrüßten sich zeit­gemäß und Vahlen betrat mit ein­er schw­eren Tasche beladen das Zim­mer. Es hat­te offen­bar mehr Ein­sendun­gen gegeben als let­ztes Mal. Vahlen holte gle­ich mehrere Stapel her­aus und bre­it­ete die etwa 500 Seit­en auf Bieber­bachs Schreibtisch aus. Bieber­bach nahm noch einen Zug von sein­er Zigarette, dann macht­en sie sich gemein­sam an die Arbeit.

Alfred Man­dl legte die Füllfed­er weg, als er den Brief an seinen Sohn sig­niert hat­te. Er ord­nete die losen Blät­ter zu einem kleinen Stapel und ließ sie in der Mitte seines Schreibtischs ruhen, mit der Fed­er oben aufliegend. Daneben, als Ver­längerung der oberen und unteren Briefkante, legte er eben­falls fein­säu­ber­lich geord­net eine Abschrift sein­er unvol­len­de­ten let­zten Arbeit. Einen Teil davon hat­te er so gut wie möglich zu einem Abschluss gebracht und in einem frankierten A4-Kuvert an sein ehe­ma­liges Insti­tut geschickt – nicht aus Trotz, nicht aus Hoff­nung, son­dern weil es das war, was er immer getan hat­te. Den Rest ließ er auf seinem Schreibtisch liegen. Die meis­ten Noti­zen hat­te er zer­ris­sen und wegge­wor­fen.

Aus den Ein­sendun­gen bilde­ten Bieber­bach und Vahlen zuerst zwei Men­gen: Die noch unbekan­nten und die bere­its bekan­nten. In der Menge der bere­its bekan­nten sam­melten sich sogle­ich die Namen einiger Autoren an, die alle schon mehrmals in den Aus­gaben der ver­gan­genen 6 Jahre pub­liziert hat­ten: Kubach, Weber, Teich­müller, Schön­hardt, Dörge, Krafft, Schulz, Tornier ... Bieber­bach kan­nte ihre Arbeit­en bere­its und wusste, dass man sie get­rost ohne weit­ere Prü­fung abdruck­en kon­nte. Die Unbekan­nten gliederten sie hinge­gen noch ein­mal in zwei Grup­pen, wobei sie nach einge­hen­der Betra­ch­tung immer wieder Kor­rek­turen vor­nah­men, die eine oder andere Arbeit doch noch ein-, zweimal in eine andere Gruppe und wieder zurück ver­schoben, je nach Ein­schätzung und immer in gemein­samer Absprache.

In den let­zten Monat­en waren die Mel­dun­gen immer drastis­ch­er gewor­den, die Empfehlun­gen und Bit­ten sein­er im Aus­land lehren­den Bekan­nten immer drän­gen­der. Vor eini­gen Wochen hat­te er sein­er Frau Mar­i­ja noch ver­sichert, dass er seit Jahrzehn­ten an der Uni­ver­sität angestellt sei. Man kenne ihn hier. Man werde ihn hier nicht so schnell wegschick­en. Er sei ein uner­set­zlich­es Mit­glied des akademis­chen Forschungsstabs.

Die Arbeit eines gewis­sen Kozlows­ki fing zuerst Bieber­bachs Blick. In sein­er Ein­leitung hat­te er die unnatür­liche Landau’sche Def­i­n­i­tion von π als die Dop­pelung der kle­in­sten pos­i­tiv­en Null­stelle der Cos­i­nus­funk­tion ver­wen­det, anstatt die nor­male und weitaus intu­itiv­er erfass­bare Beschrei­bung als Ver­hält­nis von Kreisum­fang zu Kreis­durchmess­er zu ver­wen­den. Bieber­bach zeigte Vahlen schmun­zel­nd die betr­e­f­fende Stelle, der nur kurz den Kopf schüt­telte und die 70-Seit­en lange Arbeit seufzend in den Papierko­rb warf.

Er hat­te sich immer ein kleines Haus am Strand vorgestellt. Wo er mit sein­er Frau und seinem Sohn leben würde. Ein Haus an der Nord­see, Schilf, Möwen, Salz. Er würde mit den bei­den spazieren gehen, den Strand auf und ab und die Fußab­drücke wür­den hin­ter ihnen im nassen Sand verblassen. Sein Sohn würde bis zum Hor­i­zont sehen und sich fra­gen, wie lang wohl die Küste war.

Theodor Vahlen fiel die Arbeit eines Her­rn Leit­er­mey­er in die Hände, der die unge­sunde Ange­wohn­heit entwick­elt hat­te, nach franzö­sis­ch­er Meth­ode zu abstrahieren, ohne eine prak­tis­che physikalis­che, mech­a­nis­che oder mil­itärische Anwen­dung für seine Über­legun­gen aufzuzeigen oder auch nur eine einzige andere prag­ma­tis­che App­lika­tion sein­er Arbeit anzudeuten. Nicht nur hat­te er ver­sucht, die Rie­mann-Zeta-Funk­tion – eine Funk­tion die so viele nüt­zliche, physikalis­che Anwen­dun­gen besaß! – als bloßes Werkzeug zur Erforschung der Gold­bach­schen Ver­mu­tung zu benutzen, was laut Bieber­bach das­selbe war, als würde man mit Ham­mer und Sichel ein Zwölfton­stück dirigieren, son­dern er hat­te auch immer wieder Bezug auf diesen unsäglichen Schar­la­tan Srini­vasa Ramanu­jan genom­men, der die britis­chen Uni­ver­sitäten schon seit Jahrzehn­ten zum Nar­ren hielt und sich nun nach seinem Tod offen­bar auch noch im Deutschen Reich einzuschle­ichen ver­suchte. „Nicht mit mir“, murmelte Vahlen und warf die Arbeit eben­falls weg.

Sie hat­ten den vier­jähri­gen Otto vor ein­er Woche nach Birm­ing­ham geschickt. Zuerst auf der Rück­bank des Autos eines Bekan­nten und schließlich im Kof­fer­raum. Sie hat­ten so schnell wie möglich nachkom­men wollen. Doch die Gren­zen waren dicht. Der Befehl zur Umsiedelung war vor ein paar Tagen eingetrof­fen. Er hat­te ihn mit der übri­gen Haus­post in die Woh­nung gebracht. Als ob sich der Teufel heim­lich in ihre Woh­nung geschlichen hat­te. Er wün­schte sich, er hätte den Brief überse­hen und ein­fach noch ein paar Tage in naiv­er Blind­heit ver­bracht. Er wün­schte sich, er hätte ihn zusam­men mit den Flug­blät­tern im Haus­müll entsorgt.

Endlich fiel Bieber­bach ein Manuskript in die Hände, das er nicht sofort in den Mülleimer fall­en ließ. Ein gewiss­er Herr Loth­mann hat­te einen Entwurf ein­er neuen Arith­metik, oder vielmehr ein­er neuen math­e­ma­tis­chen Meta­physik ein­gere­icht, die die anglis­tis­chen und franzö­sis­chen Abstrak­ta zurück­wies und eine völ­lig neue Art vorschlug, mit den math­e­ma­tis­chen Instru­menten umzuge­hen. Loth­mann dachte an, sämtliche Rechen­vorgänge in der ganzen math­e­ma­tis­chen Forschung und darüber hin­aus, auf die ger­man­is­chen Urze­ichen zurück­zuführen, spez­i­fisch, auf die antiken ger­man­is­chen Runen, in denen der erste arische Gebrauch von Zahlze­ichen begrün­det war. Bei jedem Rechen- oder Zäh­lvor­gang sollte diese Meth­ode Anwen­dung find­en. Wollte man beispiel­sweise fest­stellen, ob man es mit exakt 100 Stück eines Gegen­standes zu tun hat­te, so musste man die ger­man­is­che Urhun­dert kon­so­li­dieren, die auf den sagenum­wobe­nen Runen-Steinen von Hel­næs auf Fünen in Däne­mark einge­meißelt waren. Da die 100 Striche auf den Steinen die erste belegte Darstel­lung der Zahl 100 sei, müsse sich jede weit­ere Ver­wen­dung der Zahl an diesem ersten Präze­den­z­fall messen. So sei jed­er math­e­ma­tis­che Vor­gang ein direk­tes Zitat der ger­man­is­chen Vor­fahren und habe somit bere­its eine intrin­sis­che Beweiskraft, die kein ander­er Rechen­vor­gang haben könne. Loth­mann bitte das Math­e­ma­tis­che Insti­tut hier vor allem um beträchtliche Kost- und Logis-Zuschüsse für die geplanten Reisen nach Däne­mark, um jede getätigte Rech­nung mit den Strichen auf den Steinen von Hel­næs abzu­gle­ichen. Erhielt ein Math­e­matik­er auf eine Rech­nung beispiel­sweise das Ergeb­nis 27, so musste er in den Zug nach Kopen­hagen steigen, von dort eine Fähre nach Fünen nehmen und einige Kilo­me­ter zu Fuß an der Küste ent­lang laufen, bis er schließlich, an den Steinen von Hel­næs angekom­men, über­prüfen kon­nte, ob seine 27 der ger­man­is­chen Ur-27 entsprach.
Es würde einiges an Zeit und vor allem Geld in Anspruch nehmen, so Loth­mann, doch er würde die Mühen als aufrechter Patri­ot für das Heil des deutschen Vater­lan­des ertra­gen und jede einzelne Rech­nung per­sön­lich auf ihren arischen Wahrheits­ge­halt über­prüfen.
Endlich ein sin­nvoller Vorschlag! Bieber­bach nick­te anerken­nend, während er das Paper über­flog und legte es schließlich zu den Entwür­fen für das neue Mag­a­zin.
Die Arbeit eines Her­rn Rosen­berg ließ Vahlen unter­dessen schon im Mülleimer ver­schwinden noch ehe er über das Deck­blatt hin­aus war.

Das Para­dox der Küsten­lin­ie hat­te Alfred Man­dl Zeit seines Lebens nicht los­ge­lassen. Es war das, was ihn in erster Lin­ie zur Math­e­matik gebracht hat­te. Ein Sta­tis­tik­er namens Lewis Richard­son hat­te es vor cir­ca dreißig Jahren durch puren Zufall ent­deckt. Er hat­te ver­mutet, dass sich Kriege durch bloße Zahlen erk­lären ließen, durch die Anzahl der Sprachen die eine Gruppe von Län­dern sprach, durch die Anzahl der ver­schiede­nen Reli­gio­nen und Völk­er­grup­pen inner­halb eines Staates, durch die Anzahl und Verteilung der Ein­wohn­er im Ver­hält­nis zur Fläche. Durch die Anzahl und Länge der Gren­zen, die mit anderen Staat­en geteilt wur­den. Man­dl hat­te Richard­sons Auf­satz als Stu­di­en­as­sis­tent durch puren Zufall ent­deckt, als ihn die Uni­ver­sitäts­bib­lio­thekarin darum gebeten hat­te, ihr zu sagen, welche Büch­er sie weg­w­er­fen könne.
Richard­son hat­te fest­gestellt, dass ver­schiedene Staat­en völ­lig wider­sprüch­liche Infor­ma­tio­nen über die Länge ihrer Gren­zen hat­ten. Sie wichen von Sta­tis­tik zu Sta­tis­tik kom­plett voneinan­der ab. In der Tat war anzunehmen, dass das Deutsche Reich keine Ahnung hat­te, wie lang seine ständig wach­senden Gren­zen waren. Und schließlich hat­te Richard­son den Grund dafür gefun­den: Je fein­er man die Gren­zen eines Lan­des maß, je klein­er der Maßstab war, den man wieder­holt an seine Rän­der legte, je mehr kleine Fein­heit­en, Landzun­gen und Bucht­en man berück­sichtigte, desto länger wurde die Strecke. Ja in der Tat gab es keine Ober­gren­ze. Je nach Wahl des Län­gen­maßes war die Küsten­lin­ie ein­er Insel beliebig lang. Das Ergeb­nis wurde von der Mes­sung bes­timmt.

Endlich stieß Bieber­bach auf eine Arbeit, die als Titelgeschichte in Frage kam. Der Numerik­er und Wis­senschaft­sphilosoph Vik­tor Hart­mann machte bere­its im Vor­wort klar, dass er der­art absurde franzö­sis­che und jüdis­che Vorstel­lun­gen ein­er unab­hängig vom men­schlichen Ver­stand existieren­den Zahlen­welt strikt ablehne. In sein­er Arbeit wolle er deshalb ganz im Deutschen Geiste die Zusam­men­hänge zwis­chen Math­e­matik und Phrenolo­gie unter­suchen. Hierzu habe er auf his­torischen Bild­nis­sen berühmter Math­e­matik­er wie etwa Gauß, Bolzano, Möbius, Rie­mann oder Can­tor die Schädelfor­men unter­sucht und deren wis­senschaftliche und poli­tis­che Ein­stel­lun­gen mit der Inte­gra­tionsty­polo­gie des Psy­cholo­gen Erich Rudolf Jaen­sch abgeglichen, sodass man in Zukun­ft wom­öglich intu­itiv-math­e­ma­tis­che Genies und abstrahierend-volks­feindliche Kom­mu­nis­ten und Ver­räter schon allein anhand ihrer Stirn­höhe iden­ti­fizieren könne. Dies sei vor allem für die Ein­teilung in den unter­men­schlichen, intellek­tuell infe­ri­oren S-Typus und den über­lege­nen arischen J-Typus des math­e­ma­tis­chen Denkens von beson­der­er Wichtigkeit und kön­nte dem Deutschen Reich let­z­tendlich zu wis­senschaftlich­er und auch mil­itärisch­er Vorherrschaft ver­helfen, spez­i­fisch in Hin­sicht auf die Entwick­lung ein­er möglichen Wun­der­waffe, wie es die Vision des Führers sei.
Bieber­bach nick­te anerken­nend und machte einen Ver­merk, dass man die Titelgeschichte für die näch­ste Aus­gabe der Deutschen Math­e­matik gefun­den habe. Vahlen, der eben­falls beein­druckt, ja direkt von Stolz erfüllt lächelte, trug den Namen des Autors in eine Liste mit Vorschlä­gen zur Stipendi­ums- und För­der­mit­telver­gabe der Deutschen Forschungs­ge­mein­schaft ein.

Vor drei Wochen war Man­dls Vor­lesung zu iter­a­tiv­en Vek­toren­räu­men von Mit­gliedern des Nation­al­sozial­is­tis­chen Deutschen Stu­den­ten­bun­des gestürmt wor­den und er war nur um ein Haar einem faust­großen Stein ent­gan­gen, den ein nicht ein­mal 20jähriger Junge mit einem inbrün­sti­gen Schrei nach ihm gewor­fen hat­te. Anges­tachelt hat­te sie Oswald Teich­müller, ein Mann, von dem selb­st Man­dl sagen musste, dass es sich bei ihm zweifel­sohne um ein math­e­ma­tis­ches Genie han­delte, aber noch viel mehr um einen kriegs­fa­natis­chen Faschis­ten. Er war ger­ade erst von der Inva­sion in Nor­we­gen wiedergekehrt und das erste was er tat, war amerikanis­che Ver­schlüs­selun­gen zu entz­if­fern und Rie­manns The­o­rien zu lehren, ohne ein einziges Mal Rie­manns Namen zu erwäh­nen. Er sprach von Teich­müller­räu­men, von Teich­müller­flächen. Von einem Teich­mülleruni­ver­sum.
In den fol­gen­den Wochen ver­schwand neben „Rie­mann“ auch der Name „Man­dl“ aus den Vor­lesun­gen, genau wie aus den Archiv­en. Rie­manns Name sollte wieder auf­tauchen. Man­dls nicht.

Der Stein, den der Stu­dent nach ihm gewor­fen hat­te, war für ihn der let­zte Beweis gewe­sen, dass es ihn an der Uni­ver­sität gegeben hat­te. Er war an seinem Ohr vor­beig­er­auscht und hat­te eines der Fen­ster in der Seit­en­wand des Hör­saals ein­geris­sen. Die Scher­ben waren erst nach eini­gen Sekun­den auf dem Bürg­er­steig aufgeschla­gen und das Auf­prallen einzel­ner Bruch­stücke auf den Well­blechdäch­ern der park­enden Autos hat­ten sich ange­hört wie ein plöt­zlich­er Hagelschauer.
Vor ein­er Woche hat­te er erfahren, dass das math­e­ma­tis­che Gremi­um der Har­vard Uni­ver­si­ty sein Ansuchen um ein Forschungsstipendi­um abgelehnt hat­te.

Beim let­zten einge­sandten Manuskript han­delte es sich um die math­e­ma­tisch-physikalis­che Arbeit eines gewis­sen Her­rn Man­dl über die Imp­lika­tio­nen neuer Entwick­lun­gen in der Geome­trie. Der Autor ver­trat darin die völ­lig absurde Idee, dass es möglich sei, die Rel­a­tiv­ität­s­the­o­rie mit der Quan­ten­physik zu vere­inen, wenn man die Physik als Wis­senschaft auf ein Gerüst aus beweglichen, selb­stre­f­er­en­tiellen, dynamisch-flu­iden Koor­di­naten­sys­te­men stützte, die gle­ichzeit­ig eine zu beschreibende Naturkraft und ihr eigen­er, sich selb­st beschreiben­der Ref­eren­zrah­men seien. Er schwafelte von ein­er sich selb­st krüm­menden Raumzeit, die gle­ichzeit­ig ihr eigenes quan­tifiziertes Koor­di­naten­sys­tem bildete. Dieser Mann ver­suchte nichts Gerin­geres, als einen uni­ver­salen Pro­jek­tor zu bauen, der gle­ichzeit­ig das Bild war, das er pro­jizierte. Ein Raum, der sich selb­st erschuf, was so ziem­lich das welt­fremdeste war, was den bei­den Dozen­ten jemals untergekom­men war.

Man­dl wusste, dass das, was sich vor seinem Fen­ster abspielte, in erster Lin­ie ein Bedeu­tungswan­del war. Das Wort „Men­sch“ hat­te sich verän­dert. Das Wort „Volk“ hat­te sich verän­dert. Sehr viele Wörter hat­ten sich rasend schnell verän­dert. Was ihn am aller­meis­ten wun­derte, war daher diese abstruse Weigerung sein­er Kol­le­gen, anzuerken­nen, dass sich die wis­senschaftlichen Wörter eben­falls änderten. Die Wörter für Raum und Zeit. Die Wörter für Masse und Energie. Die Wörter für Ort und Moment, für Länge und Umfang.
Was sich hier ereignete, war nicht der Ver­such, eine neue Welt zu erschaf­fen, son­dern der Ver­such, die ganze Welt auszuschließen. Man wollte sich von allen Entwick­lun­gen außer­halb des eige­nen Reich­es isolieren und sie sich para­dox­er­weise den­noch voll­ständig aneignen.
Im ganzen Deutschen Reich hat­te man, ohne es auszus­prechen, beschlossen, dass man keine Wis­senschaft mehr betreiben wollte. Auch das war ein Bedeu­tungswan­del. Soll­ten die Objek­te, die man sich weigerte anzuerken­nen, eines Tages aus dem Him­mel fall­en, so würde es keine Namen dafür geben. Denn was da herun­ter­fiel und alles Leben in Reich­weite auf einen Schlag aus­löschte, kon­nte und durfte nicht existieren.

Man­dls Arbeit wurde abgelehnt. Ein­er­seits auf­grund ihrer völ­lig unre­al­is­tis­chen, abstrak­ten, undeutschen, ja gar volks­feindlichen Annah­men, die die Geset­ze der klas­sis­chen Math­e­matik und Physik in Frage stell­ten, die Vorstel­lung eines unnatür­lichen, kon­train­tu­itiv­en, imma­teriellen Uni­ver­sums propagierten und nicht zulet­zt auch wegen den diversen Ver­weisen auf einen Physik­er namens Ein­stein. So etwas hat­te keinen Platz in der Math­e­matik. Diese abstrak­ten, irreführen­den Ideen waren Ide­olo­gien des Fein­des, die das Deutsche Volk daran hin­dern woll­ten, an prak­tisch nutzbaren Phänome­nen zu forschen. Sie woll­ten die deutschen Wis­senschaftler ver­wirren und auf eine falsche Fährte lock­en, damit sie im Stillen an ihren eige­nen Waf­fen arbeit­en kon­nten. Aber die Deutsche Math­e­matik würde das ändern. Die Deutsche Math­e­matik würde die wis­senschaftliche Forschung im Großdeutschen Reich wieder auf den Boden der Tat­sachen, auf ein Fun­da­ment aus Erde, Blut und Stahl holen. Sie würde die Wis­senschaft nach Jahren der franzö­sis­chen, britis­chen und jüdis­chen Aufwe­ichung endlich wieder tief in der Ver­gan­gen­heit der arischen Rasse ver­wurzeln und die Deutsche Forschung würde zu ihrem ursprünglichen Glanz zurück­kehren. Nur so kon­nte man den Krieg gewin­nen. Nur so kon­nte man die Zukun­ft des Reich­es sich­ern.

Man­dls Traum war es gewe­sen, die gesamte Wis­senschaft auf einen neuen philosophis­chen Boden zu stellen, der von der völ­li­gen Leere der Welt aus­ging. Zu dieser Vorstel­lung ließ er sich laut einem Brief­fre­und nicht nur von den kon­tem­porären Entwick­lun­gen in der Kos­molo­gie bee­in­flussen, son­dern eben­falls von den bud­dhis­tis­chen Vorstel­lun­gen des Jen­seits, die Mitte des 20. Jahrhun­derts nach und nach Einzug in den kul­turellen West­en fan­den und über Schopen­hauer let­ztlich auch in Man­dls Lek­türe. Für Man­dl bestand kein Wider­spruch in der Tat­sache, dass nichts existiere. Für Man­dl bestand kein grundle­gen­der Fehler in der Aus­sage „1≠1“. Eine Küste hat­te keine Länge. Ein Gegen­stand hat­te keine Form. Aus Man­dls Sicht bestand zwis­chen all den Stof­fen, aus denen sich das Uni­ver­sum zusam­menset­zte, kein nen­nenswert­er qual­i­ta­tiv­er Unter­schied.

Let­zte Nacht hat­te er geträumt, er ste­he in ein­er weißen Land­schaft. Sie war flach, voll­ständig kon­tur­los und ver­lief in alle Rich­tun­gen, soweit das Auge sehen kon­nte. Er schritt die Fläche in mehrere Rich­tun­gen stun­den­lang ab und kon­nte nicht fest­stellen, dass sich irgen­det­was an ihr verän­derte. Der Boden unter seinen Schuhen war hart wie ein Bürg­er­steig, aber auch dort kon­nte er keine For­men erken­nen. Der Boden hat­te abso­lut keine Eigen­schaft.
Mit­ten in der Nacht war er schweiß­durch­we­icht aufgeschreckt und hat­te panisch nach einem Blatt Papi­er und einem Bleis­tift gegrif­f­en. Inner­halb weniger Minuten hat­te er seine The­o­rie der selb­stre­f­er­en­tiellen Koor­di­naten­sys­teme notiert. Eine Ontolo­gie von Gegen­stän­den, die ihren eige­nen Bezugsrah­men darstell­ten. Eine Welt von Objek­ten, die alle flu­ide ineinan­der übergin­gen, sich gegen­seit­ig bee­in­flussten und sich dabei selb­st in jed­er Einzel­heit beschrieben. Nach­dem er zehn Seit­en vollgeschrieben hat­te, ließ er den Stift fall­en und schlief völ­lig erschöpft ein.
Am näch­sten Mor­gen las er sich die Seit­en durch, schüt­telte den Kopf und zer­riss das Papi­er in kleine Fet­zen. Er stand auf, trank einen Kaf­fee und ging zu seinem Hausarzt, dem er erk­lärte, dass er seit Wochen unter Schlaf­prob­le­men lei­de, was nicht ein­mal gel­o­gen war. Er stellte ihm ein Rezept für ein Fläschchen Bar­bi­tal-Tablet­ten aus. Die Apothek­erin, bei der er das Medika­ment holte, hat­te ihn mitlei­dig ange­se­hen und ihm gute Besserung gewün­scht. Sie hat­te ihm beim Ver­ab­schieden zugelächelt als würde sie seinen Namen ken­nen.

Bieber­bach nahm einen let­zten Zug von sein­er Zigarette, blies den Rauch genüsslich über sein Werk und drück­te den glim­menden Stum­mel in der Con­clu­sio von Man­dls Arbeit aus, wo sie ein tiefes Brand­loch in den the­o­retis­chen Grund­la­gen zur Her­stel­lung ein­er uran­freien Atom­bombe hin­ter­ließ. Dann machte er das Fen­ster auf und ließ die Wärme der Maisonne und den Duft der Sil­ber­lin­den in seine Garçon­nière. Die Auswahl für die let­zte Aus­gabe des Mag­a­zins Deutsche Math­e­matik war abgeschlossen.

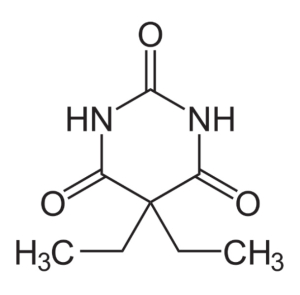In einem sein­er alten Lehrbüch­er für chemis­che Math­e­matik hat­te Man­dl die Struk­tur­formel von Bar­bi­tal nachgeschla­gen und fest­gestellt, dass es eine per­fek­te Rechts-Links-Sym­me­trie hat­te. Der zen­trale hexag­o­nale Kar­bon­ring wurde von zwei Stick­stoffatomen flankiert, drei dop­pelt gebun­dene Sauer­stoffatome umkreis­ten ihn als per­fek­tes gle­ich­seit­iges Dreieck und zwei abste­hende Kar­bon­grup­pen mit je drei Wasser­stoffatomen lagen zu seinen Füßen. Etwas an dem har­monis­chen Auf­bau und der naiv­en Vorstel­lung von klar getren­nten, ewigen Ein­heit­en mit homo­ge­nen, absoluten Bindun­gen zwis­chen sich, wirk­te auf ihn beruhi­gend und seine Hände zit­terten ein kleines biss­chen weniger, als er damit begann, die weißen Tablet­ten mit der Rück­seite eines Löf­fels zu zerklein­ern, ehe er das Pul­ver auf zwei Gläs­er verteilte.
Sein Sohn hat­te ihn nie gefragt, wie lang die Küste war.
Er hat­te ihn gefragt, wie weit Birm­ing­ham von Berlin ent­fer­nt ist.
Es sind 982 Kilo­me­ter.

Es war der 17. Mai des Jahres 1942. Die Welt war drei­di­men­sion­al. Raum und Zeit waren unverän­der­liche Felsen in der Bran­dung. Das Exper­i­ment ging stets der The­o­rie voraus. Der Wel­traum bestand aus Eis, Met­all und Äther. Alle Vorgänge in der Welt waren kon­stant und kon­nten kausal, phänom­e­nol­o­gisch und intu­itiv vom men­schlichen Geist erfasst wer­den. Der Men­sch war ein blonder, blauäugiger, blutrein­er, nordis­ch­er Mann. Das öffentliche Leben in Hiroshi­ma und Nagasa­ki ver­lief den Umstän­den entsprechend nor­mal und das Deutsche Reich würde 1000 Jahre lang beste­hen.